Data partitioning: Consistent-Hashing

Overview

From the previous article we may already have a basic concept of the load balancer, this time, let’s look at one of the popular algorithm: Consistent Hashing

Use Cases

Consistent Hashing is quite useful when dealing with the cache distributed issue in a dynamic environment (The servers keep adding/removing) compares with the Mod-Hashing.

Basically, it maps keys and values into the same hash ring circle, it can be implemented via a hash-function + binary-search. Additionally, we will bring the virtual nodes to overcome the unbalancing issue when the servers be added or removed.

Case	Products	Notes
Auto data partition	Couchbase
	OpenStack\’s Object Storage
	Dynamo	Amazon\’s K-V storage
	Apache Cassnadra
Distributed Cache	Akka\’s router

The Motivation

If we have 4 cache servers (index: [0,1,2,3]), the different server maintains different cache data and the routing formula is the basic Mod-Hashing: p = h(x) % 4. Then, if the server 2 is down, according to the formula we will have: p = h(x) % 3.

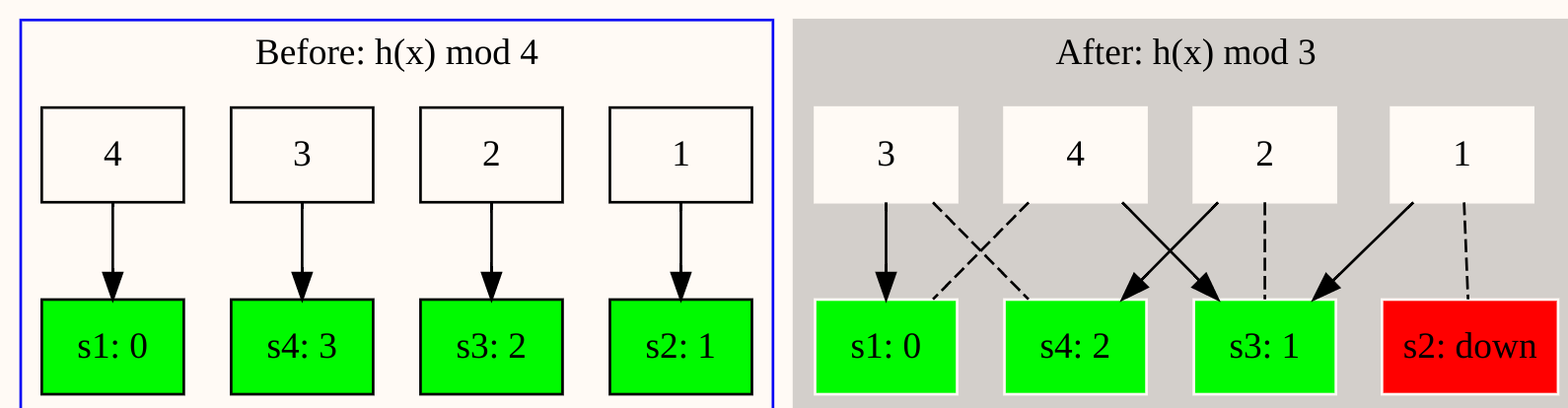
From above, we can clearly see that, if the server 2 is down, all requests will be re-routed to a different server, it will cause the cache on the server are all invalid.

Basically we want to minimize the impact of the cache hit rate when add/remove nodes.

Follow up:

• What if server 1, 3 or 4 is down?

Let’s see:

• Server 1 down? 4 requests are re-routed.
• Server 2 down? 4 requests are re-routed.
• Server 3 down? 3 requests are re-routed. (req [2,3,4])
• Server 4 down? 2 requests are re-routed. (req [3,4])

Now, we have a formula to calculate how many nodes be impacted: n = T - \max(ServerIdx - 1, 0)

Where:

• n: number of nodes impacted
• T: Total number of servers
• ServerIdx: The server at ServerIdx is down

In order to solve the problem, the consistent-hashing comes to the picture, with:

• Add a node: 1 / n + 1 data will be moved to the new node
• Remove a node: 1 / n data will be redistributed to all other nodes

How it works

The idea is quite simple, hash the requests and server nodes in the same hash ring circle, then whenever the server nodes changes, the most of the requests will remain the same routing path, only a very small part of requests will be remapped, which is friendly to the cache likely service.

Let’s say we only have two nodes a and b, for each node, we hash its unique nodeId then get hashcodes ha = 100 and hb = 200, now we put it into a circle range [0, 255], then if any request incoming, we apply the same hash function to get a hashcode r1 = 150, by having this hashcode, we find which node is the next closest node in the clockwise order, in this case, the next one is node b due to its hashcode is 200.

Then if we add a new node c (hashcode is 150), then only those requests are hashed in the range [101, 150] will be mapped to the node c, all other requests will be remain the same path.

Checklist

Once we decide to use it, we can review and define the thresholds from below checklist first:

1. Replicas per node (1:1, 2:1, …, or 10:1), details in the Virtual-Node section
2. Data range (e.g. [0, 256] or [0, 2^32], …)
3. Hash function
4. Hash dimension
   • For queries: requestId, userId, …
   • For nodes: unique nodeId/nodeName + replicaId

Example Case

We have 3 nodes(no replicas), and we define:

• Replicas per node: 0
• Data range: 256
• Hash function: uniform hash
• Hash Dimension:
  • For queries: requestId
  • For nodes: unique nodeId + replicaId (Here we don’t have)

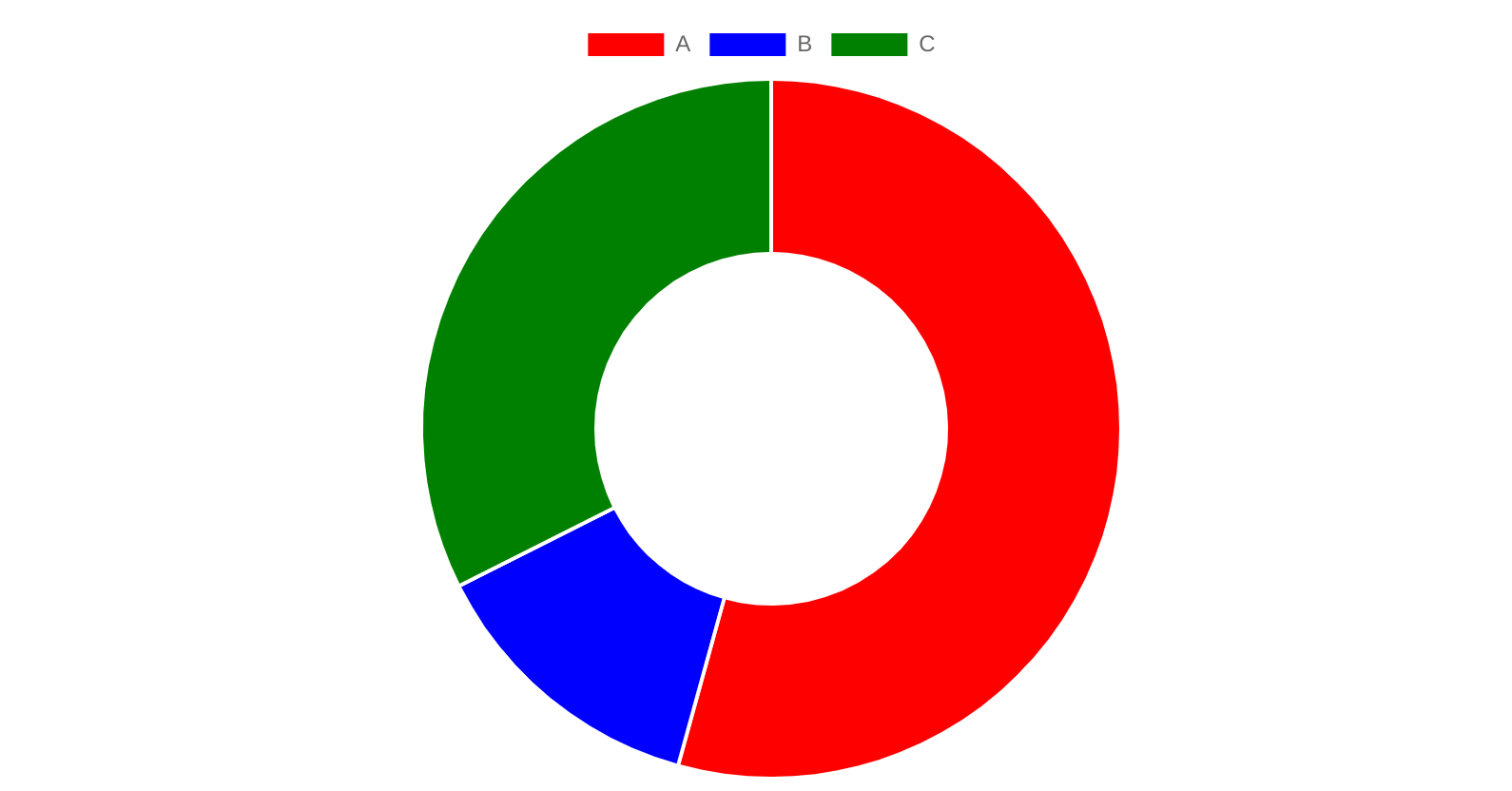
Then we hash each node on to the circle, assume we have:

Node	NodeId	Hash Value	Routing Range	Routing Weight
A	1	30	148 – 255, 0 – 30	139
B	2	64	31 – 64	34
C	3	147	65 – 147	83

Now initially, we have a hash ring circle like below:

Add Node

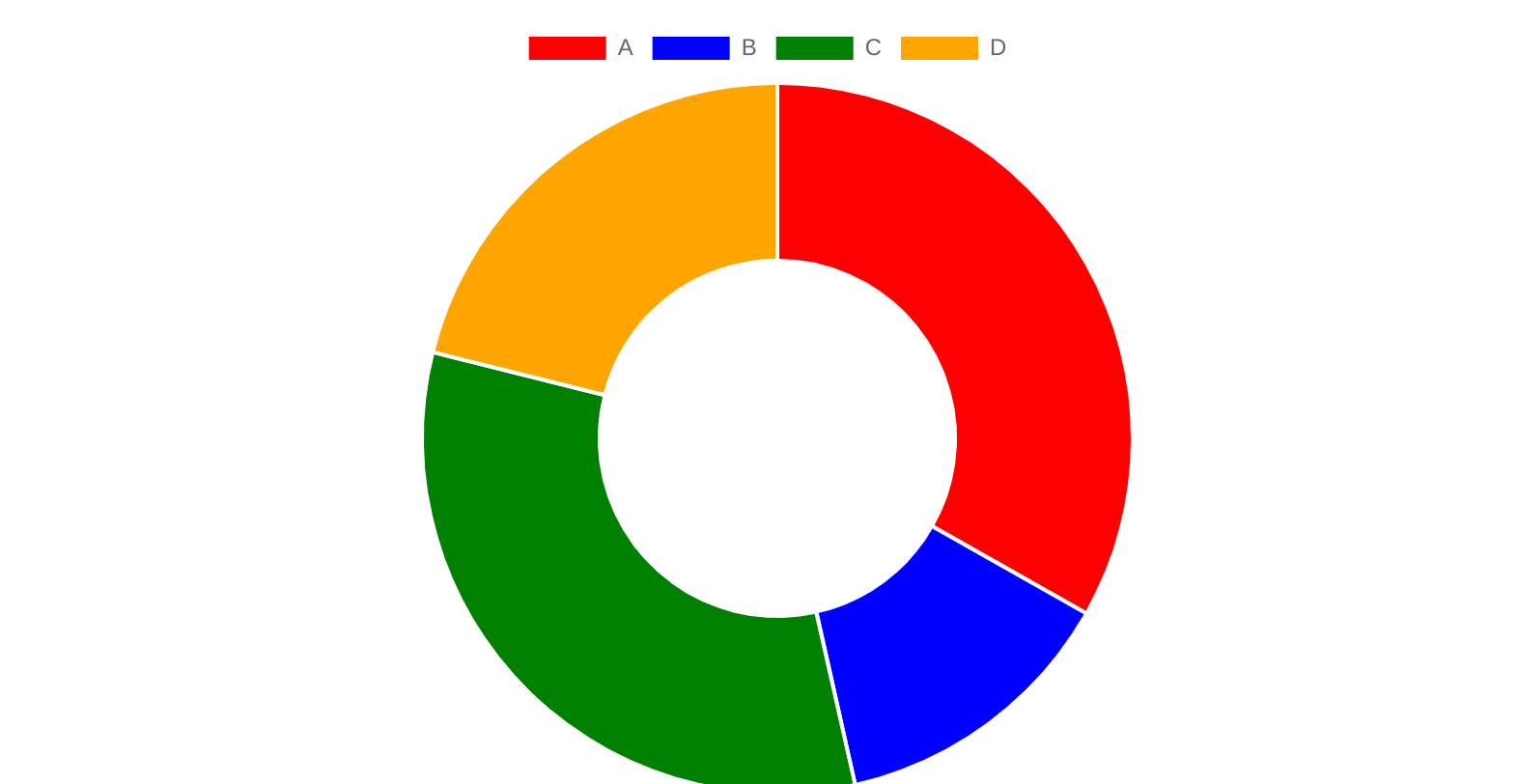
Let’s add one more node D into the system:

Name	NodeId	Hash Value	Routing Range	Routing Weight
A	1	30	202 – 255, 0 – 30	85
B	2	64	31 – 64	34
C	3	147	65 – 147	83
D	4	201	148 – 201	54

Method	Time Complexity
No Replica	O(logN)
R Replica(s)	O(RlogNR)

After adding a new node, now the hash ring becomes:

Find Node

For a request, for example, we use requestId as the dimension we want to hash:

1. Take it into the hash function f(x), get a hash value y
2. Take y to do a binary search on the circle range to find the lower-bound of node Ki
3. Query the key-node mapping to get the actual node (here since we don’t have replica, so the Ki is the node)

Examples:

Hash-Value mod 256	Route-To
10	A
200	A
40	B
100	C

Complexity:

Method	Time Complexity
No Replica	O(logN)
R Replica(s)	O(logNR)

Where:

• N: number of the nodes
• R: number of the replicas per node

Remove Node

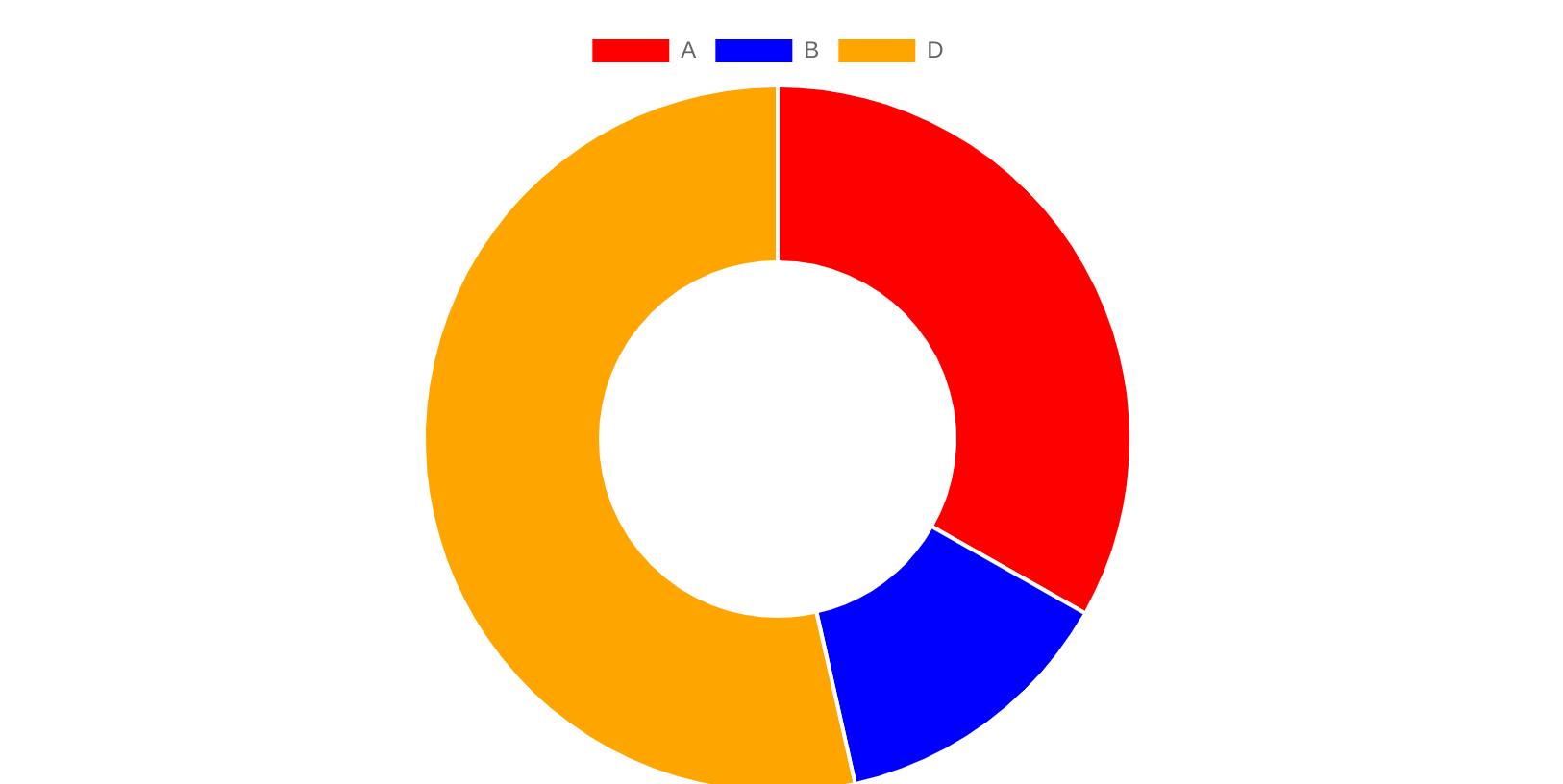
Let’s remove a node C from the system:

Name	NodeId	Hash Value	Routing Range	Routing Weight
A	1	30	202 – 255, 0 – 30	85
B	2	64	31 – 64	34
~~C~~	~~3~~	~~147~~	n/a	n/a
D	4	201	65 – 201	137

Method	Time Complexity
No Replica	O(logN)
R Replica	O(RlogNR)

After removal, the hash ring circle looks like below:

Virtual Node

Still, let’s say we have 4 nodes: n_a, n_b, n_c, n_d, let’s assume if the replica:node is the1:1, based on the algorithm above: If we remove a node n_b , then all previous requests which mapped to n_b will be remapped to the next one n_c, so n_c now is taking 2x load than others, but all others are still the same load.

In the worst case, the n_c cannot handle the 2x load, then it’s down quickly, so the next node n_d will taking 3x load, which expected to be down soon as well. (We assume all the hardwares are the same for the 4 nodes)

Snow Crash

To deal with the unbalanced load or avoid Snow Crash, people introduced virtual node into the consistent hashing algorithm.

Instead of keep key:node is always 1:1, We assign multiple keys per node, either fixed or dynamic ratio:

• A fixed n:1 ratio: Like 3 keys per node
• A dynamic ratio: node1 : [r1, r2, r3], node2 : [r4, r5]

So that, every time when we:

• Add a node: Add multiple keys into the hash ring circle, which mixed into the current keys evenly.
• Remove a node: Remove the corresponding keys from the hash ring circle.

A practical number of the virtual node is a number in the range of [100, 300]

Like this:

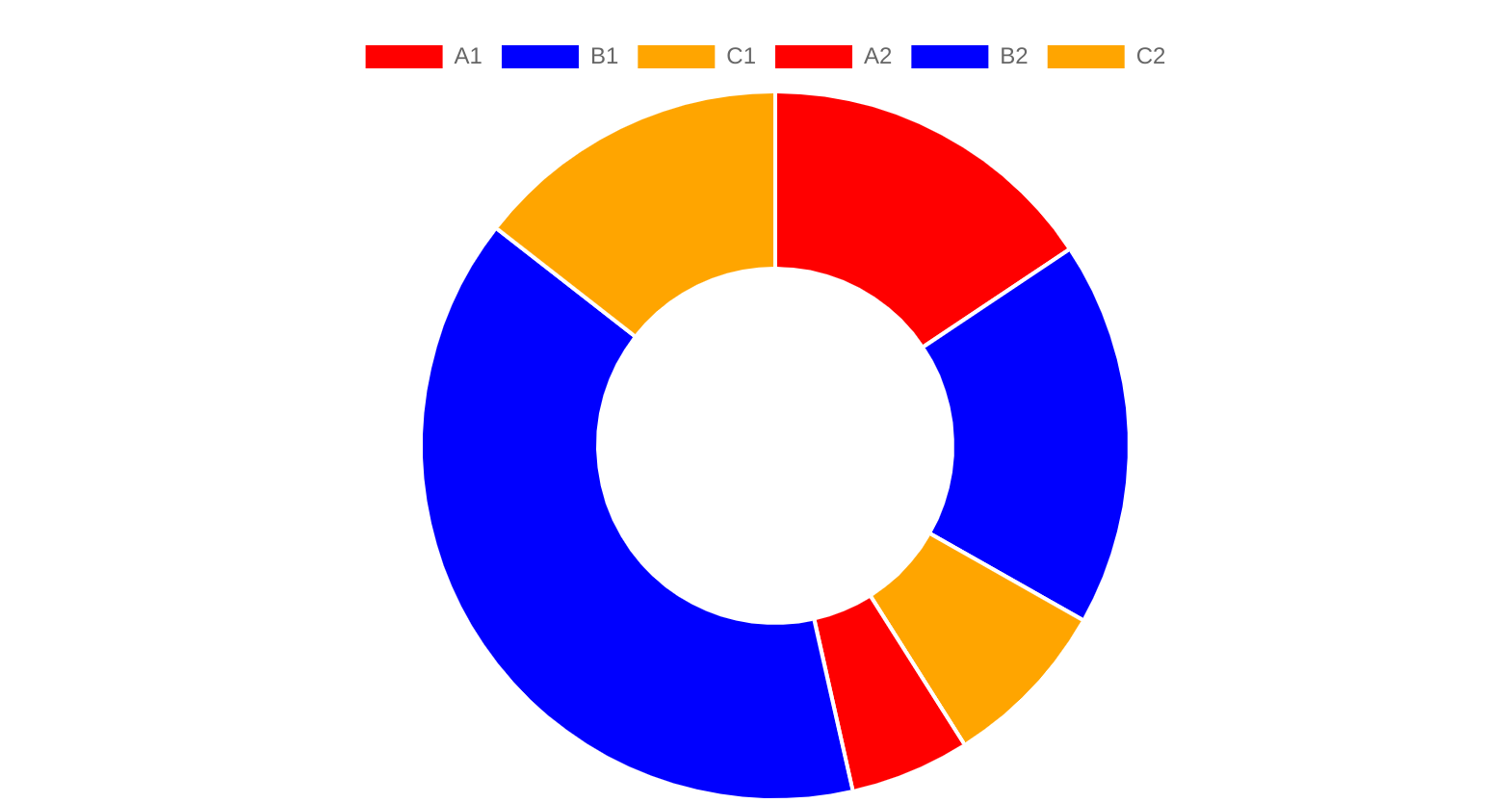
The method to add more virtual nodes are quite straight-forward, one example
is, we took NodeId_ReplicaId string into the hash function f{x}, then the
hash value y will be the hash code for this node-replica.

Complexity

Action	Time Complexity
Add a node	O(Rlog(RN))
Rmove a node	O(Rlog(RN))

Where:

• R: Number of replicas per node
• N: Number of nodes

Tweak The Replicas

Even with virtual nodes(replicas) we may still face the unbalancing issue, ideally, the replicas number in [100, 300] could be a fit for most of the product, but it’s still preferred to do an offline analysis and an online A/B test according to the different product, then we can choose the right number before releasing it into the production.

In order to have a quick sense, there is a Video I made, we can see our cluster performs good or bad in the 3 cases (replicas = 200, 400, 600).

Implementation

Below is a simple example code to show the basic idea.

C++

#define HASH_RING_SZ 256

struct Node {
  int id_;
  int repl_;
  int hashCode_;
  Node(int id, int replica) : id_(id), repl_(replica) {
    hashCode_ =
      hash<string>{} (to_string(id_) + "_" + to_string(repl_)) % HASH_RING_SZ;
  }
};

class ConsistentHashing {
private:
  unordered_map<int/*nodeId*/, vector<Node*>> id2node;
  map<int/*hash code*/, Node*> ring;

public:
  ConsistentHashing() {}

  // Allow dynamically assign the node replicas
  // O(Rlog(RN)) time
  void addNode(int id, int replica) {
    for (int i = 0; i < replica; i++) {
      Node* repl = new Node(id, replica);

      id2node[id].push_back(repl);
      ring.insert({node->hashCode_, repl});
    }
  }

  // O(Rlog(RN)) time
  void removeNode(int id) {
    auto repls = id2node[id];
    if (repls.empty()) return;

    for (auto* repl : repls) {
      ring.erase(repl->hashCode_);
    }

    id2node.erase(id);
  }

  // Return the nodeId
  // O(log(RN)) time
  int findNode(const string& key) {
    int h = hash<string>{}(key) % HASH_RING_SZ;

    auto it = ring.lower_bound(h);
    if (it == ring.end()) it == ring.begin();

    return it->second->id;
  }
};

References

• Consistent Hashing – Wikipedia
• Consistent Hashing by Michael Nielsen on June 3, 2009